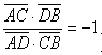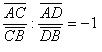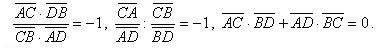Семинар ДООМ: Урок-лекция "Гармонические четверки точек. Их свойства"

Автор: Шувалова Ю.Г.

Тема урока: Гармонические четверки точек. Их свойства.

Класс: 8-9 (углубленное изучение)

Тип урока: урок-лекция изучения нового материала.

МАТЕРИАЛ К УРОКУ

Введем обозначения: AB, CD (со стрелкой) – ненулевые коллинеарные векторы; AB, CD (с чертой)– их длины, взятые с одинаковыми знаками, если векторы сонаправлены, и с разными знаками, если они противоположно направлены. Тогда, в частности, выражения и будут представлять отношение и произведение, взятые со знаком «+», если векторы сонаправлены, и со знаком «–»,они противоположно направлены.

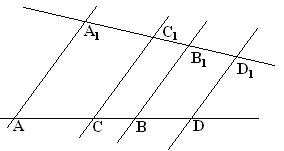
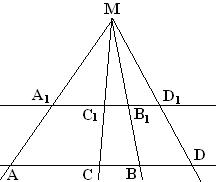
Воспользуемся принятыми обозначениями для определения гармонических четверок точек. Рассмотрим четыре точки А, В, С, D, лежащие на одной прямой. Будем говорить, что точки А, В, С, D (взятые в том же порядке, как указано) образуют гармоническую четверку, если

(*)

Из равенства следует, что среди данных векторов три вектора сонаправлены, а четвертый вектор направлен противоположно по отношению к ним.

Отметим, что данное равенство равносильно каждому из следующих равенств:

Можно написать еще несколько равенств, равносильных (*).

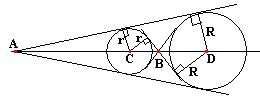
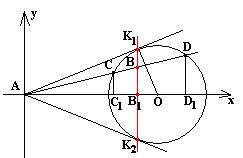
Задача: К двум окружностям разных радиусов, расположенным вне друг друга, проведены две внешние и две внутренние общие касательные. Внешние касательные пересекаются в точке А, внутренние – в точке В, точки С и D – центры окружностей. Доказать, что точки А, В, С, D образуют гармоническую четверку.

Решение: Точки А, В, С, D лежат на одной прямой. Радиусы окружностей обозначим r, R. Тогда, используя подобие прямоугольных треугольников, получаем длины векторов АС:АD=r:R и длины векторов DВ:СВ=-r:R. Отсюда следует, что . Это равенство равносильно равенству (*), а это означает, что точки А, В, С, D образуют гармоническую четверку.