Семинар ДООМ ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР С ПОМОЩЬЮ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Конспект урока
Тема: «ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР С ПОМОЩЬЮ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА» (11 класс)
Автор: Ольга Владимировна Волкова, учитель математики и информатики
Цель:
образовательная - изучение правила нахождения площади плоских фигур более сложного вида с помощью определенного интеграла
развивающая - формирование навыка рационального решения задач; развитие творческих способностей у учащихся, информационной и коммуникативной компетентности
воспитательная – формирование навыка взаимоконтроля, развитие самостоятельности, толерантного отношения к другому человеку
Тип урока: объяснение нового материала
Оборудование: проектор, ноутбук, карточки-билеты, линейка, цветные мелки
Продолжительность: 2 урока
Структура урока
- Организационный момент (2 мин)
- Проверка домашнего задания (10 мин)
- Изучение нового материала (28 мин)
- Закрепление изученного материала (35 мин)
- Домашнее задание (5 мин)
- Итог урока (5 мин)
1. Организационный момент
Сегодня на уроке мы рассмотрим площади плоских фигур, с некоторыми вы знакомы из планиметрии (Вопрос: как найти площадь треугольника, параллелограмма, прямоугольника, трапеции, круга, ромба, квадрата?), а также на предыдущем уроке. А как же находить площади остальных фигур? Ответ на данный вопрос мы будем искать вместе. Обратите внимание на доску. На ней записан план урока.
2. Проверка домашнего задания
С помощью проектора на экран высвечивается полное решение домашнего задания. Учащиеся обмениваются тетрадями и проверяют д/з друг у друга, сверяя с правильным решением, затем выставляют отметку по следующей шкале: 0 ошибок – «5», 1, 2 ошибки – «4», 3 – «3», 4 и более – «2».
В это же время 4 человека у доски готовят ответы на вопросы по билету, который они вытянули. Ответы по билетам и выставление отметки с комментарием. Правильные ответы 2 задания
Билет 1. а 0, б 2, в -4/16
Билет 2. а 0 б -1 в 2целых11/12
Билет 3. а 0 б 1 в 1,7
Билет 4. а 0,4 б корень квадратный из 3 в 6целых 1/4
3. Изучение нового материала
Выступление учащегося с докладом по исторической справке (презентация)
Работа в группах
На экран выводится презентация "Вычисление площадей плоских фигур"
Задание 1. Поставьте в соответствие фигуру и формулу нахождения ее площади.
На экран высвечивается слайд с заданием. Минута на обсуждение и заслушивается ответ каждой группы с записью на доске. Сравнение с правильными ответами.
Какой фигуре не досталась формула? Является ли она криволинейной трапецией?
Задание 2. По известным формулам попробуйте вычислить площади фигур, закрашенных синим цветом. На экран высвечивается слайд с заданием.
Пять минут на обсуждение и заслушивается ответ каждой группы с записью на доске. Сравнение с правильными ответами.
(1: S прям – S кривол.тр. = 16 – 4 = 12, 2: S верхней кривол.тр.- S нижней кривол.тр. = 24-7,5=13,5, 3: S верхней кривол.тр.- S нижней кривол.тр. = 33 - 12,5 = 45 ).
Физпауза
Задание 3. Что общего в нахождении площадей фигур задания 2?
Если одну функцию обозначить через y=f(x), а другую y=g(x), то, как можно вычислить площадь фигуры, ограниченной графиками этих функций и прямыми х=а и х=b?
Минута на обсуждение и заслушивается ответ каждой группы с записью на доске. Сравнение с правильным ответом. На экран высвечивается слайд
Задание 4. Составьте алгоритм нахождения площади плоских фигур более сложного вида с помощью определенного интеграла.
Минута на обсуждение и заслушивается ответ каждой группы с записью на доске. Сравнение с правильным ответом. На экран высвечивается слайд
Рассматриваем пример решения задачи, используя составленный алгоритм. Пример. Вычислите площадь фигуры, ограниченной прямой y=x-2 и параболой y=x2- 4x+2. На экран высвечивается слайд
4. Закрепление изученного материала
Каждый номер решает у доски один ученик
№1037(в,г)
В)
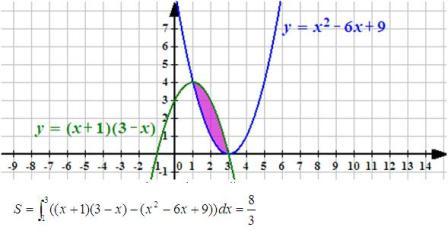 Точки пересечения графиков функций:
Точки пересечения графиков функций:
x2- 6x+9=(х+1)(3-х)
х1=1 х2=3
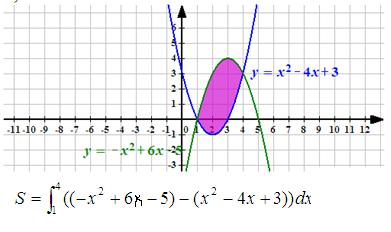
Точки пересечения графиков функций:
x2- 4x+3= -x2 +6x-5
х1=1 х2=4
№1038(в,г) В)
№1048(б,в) Б)
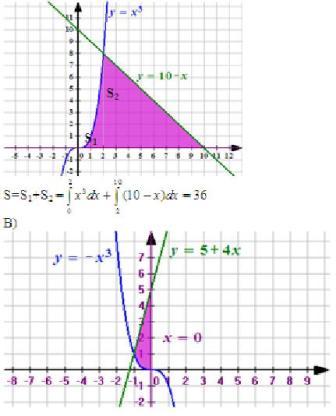
Точки пересечения графиков функций:
x3= 10-x
Т.к. одна функция возрастающая, а другая убывающая, то одна точка пересечения х=2
Проверка: 23=10-2, 8=8 – верно 10-х=0, х=10
Точки пересечения графиков функций: -x3= 5+4x
Т.к. одна функция возрастающая, а другая убывающая, то одна точка пересечения х=-1
Проверка: -(-1)3=5+4•(-1)
1=1 - верно
5. Домашнее задание
§38 п.4 стр.228-230 (учебник), №1037(а,б)-для всех, 1038 (а,б)-для всех, 1048 (а,г)- для учащихся группы А, №1049 (а,б)-для учащихся группы В, №1051(а,б)-для учащихся группы С. Все номера сопровождаются комментариями.
6. Итог урока
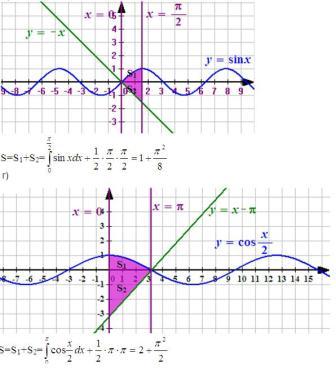
На экран высвечивается слайд. Фронтальный опрос: как найти площади изображенных фигур?