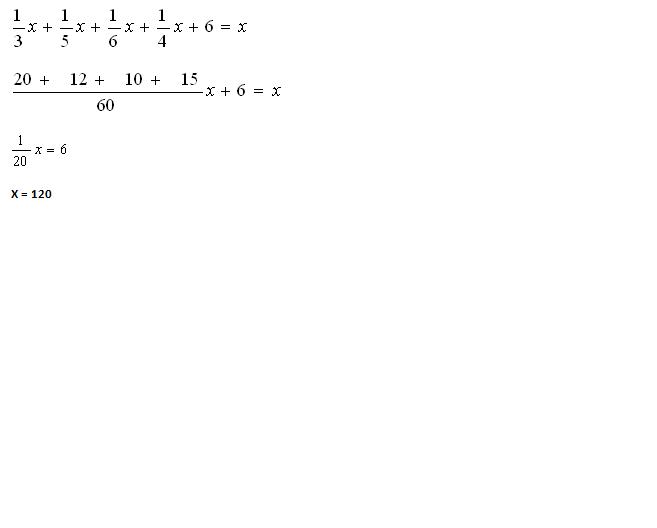Копилка знаменитых задач продолжение

Посмотреть страницу Копилка знаменитых задач. Если вы увидите сообщение что количество опубликованных знаков превышает длину страницы, то вы можете разместить свои задачи на странице Копилка знаменитых задач продолжение 3

---

Задачи участников ДООМ

ЛАДА-ВЕКТОР

1. Задача индийского математика XII в. Бхаскары.

На берегу реки рос тополь одинокий. Вдруг порыв ветра его ствол надломил. Бедный тополь упал. И угол прямой с теченьем реки его ствол составлял. Запомни теперь, что в том месте река в четыре лишь фута была широка. Верхушка склонилась у края реки. Осталось три фута всего от ствола. Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?

Решение:

Дано:

треугольник ACD – прямоугольный,

АС = 3 фута,

AD = 4 фута.

Найти: АВ.

Решение:

АВ = АС + СD; ВС = СD;

CD ² = AC x² + AD x² (по теореме Пифагора),

CD x² = 3 x² + 4 x², CD x² = 25, CD = 5 (Ф);

АВ = 3+5 = 8 (Ф).

1 фут (1 Ф) ~ 30,5 см.

Ответ: 8 футов или ~ 244 см.

2.Решение древнекитайской задачи

В клетке находятся фазаны и кролики. Известно, что у них 35 голов и 94 ноги. Узнайте число фазанов и число кроликов.

Решение:

I способ Так решали в древнем Китае.

Представим, что наверх клетки, в которой сидят фазаны и кролики, мы положим морковь. Все кролики встанут на задние лапки, чтобы дотянуться до моркови!

1) Сколько ног в этот момент будет стоять на земле?

35 2=70 (ног).

2) Но в условии даны 94 ноги, где же остальные? Это передние лапы кроликов:

94 – 70= 24.

3) Сколько же кроликов?

24: 2 = 12.

4) Сколько фазанов?

35 – 12 = 23.

Ответ: 12 кроликов и 23 фазана.

II способ решения:

Пусть х – число фазанов, у – число кроликов. Всего у них 35 голов и 94 ноги. Значит,

х + у = 35

2х + 4у = 94. Умножим все члены уравнения на 2 и вычтем первое уравнение из второго.

2х + 2у = 70

2х + 4у = 94

2у = 24

у = 12

В клетке было 12 кроликов.

х = 35 – у

х = 23

Было 23 фазана.

Ответ: 23 фазана и 12 кроликов.

3. Задача на применение теоремы Пифагора (Арабский математик XI век)

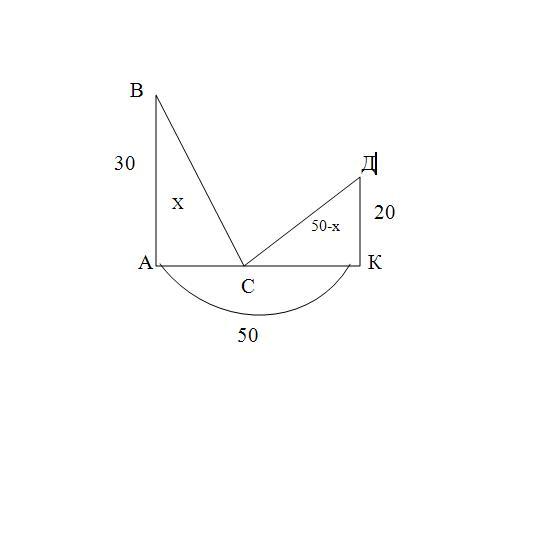
На обоих берегах реки растет по пальме, одна против другой. Высота одной-30 локтей, другой -20 локтей; расстояние между их основаниями- 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, всплывшую к поверхности воды между пальмами; обе кинулись к ней разом и достигли её одновременно. На каком расстоянии от основания более высокой пальмы появилась рыба?

Решение:

Сделаем рисунок:

Расстояние от основания более высокой пальмы до места появления рыбы, обозначим основания х. тогда расстояние до более низкой пальмы (50-х) локтей, т.к. известно расстояние между ними – 50 локтей.

Рассмотрим прямоугольные треугольники: ABC и KDC.

АВ= 30 локтей, КД= 20 локтей, АС= х локтей, КС=(50-х) локтей, ВС=ДС, т.к. птицы достигли рыбы одновременно.

Применяя теорему Пифагора.

АВ x² +АС x² = ВС x² и КД x² +КС x² =ДС x², т.к. ВС=ДС, то ВС x² =КД x² +КС; x² 30 x² +х =20 x² +(50-х) x²; 900+х x² =400+2500-100х+х x²; х=20 Ответ: 20 локтей.

4.Задача на числа (Диофант, III в.)

Найдите 2 числа, зная, что их сумма равна 20, а произведение 96.

1 способ решения:

Первое число обозначим х, второе у и составим систему уравнений; т.к. сумма чисел равна 20, то: х + у = 20; произведение 96, то х у = 96, т.е

Используя т.Виета:

х = 12; у = 8 или х =18; у = 12.

Ответ: 8 и 12.

2 способ решения:

Первое число обозначим х, второе (20-х), т.к. сумма чисел равна 20. Зная их произведение, составим уравнение:

х (20-х) = 96; х -20х+ 96 = 0

Используя т.Виета:

х=8

х=12.

Ответ: 8 и 12.

5.Задача на дроби (Бхаскары; Индия,XII в.)

Из множества чистых цветков лотоса были принесены в жертвы: Шиве- 3 доля этого множества; Вишну-пятая и Солнца- шестая; четвертую долю получил Бхавани, а остальные шесть цветков получил уважаемый учитель. Сколько было цветков?

Решение:

Пусть всего цветов было х.

Шива получил третью долю из всего множества, т. е. 1х/4.

Зная, что ещё цветков получил уважаемый учитель, составим уравнение:

Ответ: 120 цветков.

6.Задача на составление системы уравнений (Старинная задача).

Лошадь вместе с седлом стоит 235 рублей; лошадь же вместе со с рубей стоит 250 рублей; сбруя же с седлом стоит 135 рублей. Что стоит лошадь, что седло, что сбруя?

Решение:

Решим задачу с помощью системы уравнений. Пусть х

Возьмём за х рублей стоимость лошади, у рублей – сёдла, я рублей – сбруи. По условию:

x+y=235;

x+y=250;

y+z=135;

Вычитаем из первого уравнения второе:

x+y-x-z=235-250;

y=z-15;

Подставим полученное выражение в третье уравнение:

z-15+z=135;

z=75;

Найдём у:

у = z- 15=75-15=60;

Найдём х:

х + 60=235;

х=175.

Ответ: 175 рублей, 60 рублей, 75 рублей.

7.Вознаграждение воина.

Задача из «Полного курс чистой математики , сочиненный Артиллерии Штык-Юнкером и Математики партикулярным Учителем Ефимом Войтяховским в пользу и употребление юношества и упражняющихся в Математике» (1795г)

Служившему воину дано вознаграждение за первую рану 1 копейка, за другую -2 копейки, за третью – 4 копейки и т.д. По исчислению нашлось , что воин получил всего вознаграждения 655 руб. 35 коп. Спрашивается число его ран.

--Лада-Вектор ID 279 15:40, 24 октября 2008 (SAMST)

--Сталкера задач ID 219 16:11, 24 октября 2008 (SAMST)

Вопросил некто некоего учителя: "Сколько имеешь учеников у себя,так как хочу отдать сына к тебе в училище". Учитель ответил: "Если ко мне придет учеников еще столько же, сколько имею, и полстолько, и четвертая часть, и твой сын, тогда будет у меня учеников 100." Сколько было у учителя учеников?

Решение:

2х+1/2*х+1/4*х+1=100, х=36

Ответ: 36.